0723. Candy Crush¶
This question is about implementing a basic elimination algorithm for Candy Crush.
Given a 2D integer array board representing the grid of candy, different positive integers board[i][j] represent different types of candies. A value of board[i][j] = 0 represents that the cell at position (i, j) is empty. The given board represents the state of the game following the player's move. Now, you need to restore the board to a stable state by crushing candies according to the following rules:
- If three or more candies of the same type are adjacent vertically or horizontally, "crush" them all at the same time - these positions become empty.
- After crushing all candies simultaneously, if an empty space on the board has candies on top of itself, then these candies will drop until they hit a candy or bottom at the same time. (No new candies will drop outside the top boundary.)
- After the above steps, there may exist more candies that can be crushed. If so, you need to repeat the above steps.
- If there does not exist more candies that can be crushed (ie. the board is stable), then return the current board.
You need to perform the above rules until the board becomes stable, then return the current board.
Example:
Input:
board =
[[110,5,112,113,114],[210,211,5,213,214],[310,311,3,313,314],[410,411,412,5,414],[5,1,512,3,3],[610,4,1,613,614],[710,1,2,713,714],[810,1,2,1,1],[1,1,2,2,2],[4,1,4,4,1014]]
Output:
[[0,0,0,0,0],[0,0,0,0,0],[0,0,0,0,0],[110,0,0,0,114],[210,0,0,0,214],[310,0,0,113,314],[410,0,0,213,414],[610,211,112,313,614],[710,311,412,613,714],[810,411,512,713,1014]]
Explanation:
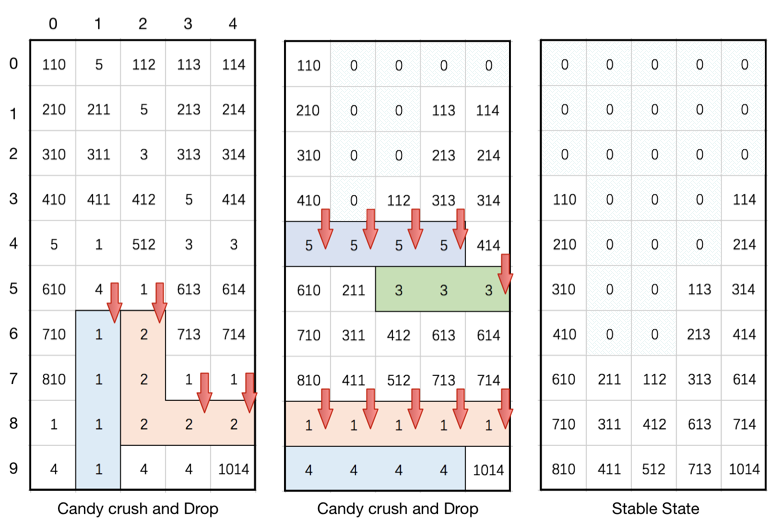
Note:
- The length of
boardwill be in the range [3, 50]. - The length of
board[i]will be in the range [3, 50]. - Each
board[i][j]will initially start as an integer in the range [1, 2000].
Analysis¶
There are three cases will cause a "crush":
- Vertically aligned with three same candies
- Horizontally algined with three same candies
- After "fell down" by gravity, above two cases could possibly happen again. Note that we don't need to write another helper function for checking if the current state is stable or not, because the check is essentially the same logic as the next call to the function (so we use recursion)
We just need to follow these three cases to write the code. Note that for step 3, we need to use the same logic after we have fallen down all the candies, thus we need to use recrusion for that case.
Code¶
class Solution {
public:
vector<vector<int>> candyCrush(vector<vector<int>>& board) {
int m = board.size();
if (m == 0) return board;
int n = board[0].size();
if (n == 0) return board;
bool todo = false;
// step 1: mark all three-algined candy to negative with **up and down** directions
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n-2; ++j) {
int v = abs(board[i][j]);
if (v != 0 && v == abs(board[i][j+1]) && v == abs(board[i][j+2])) {
board[i][j] = -v;
board[i][j+1] = -v;
board[i][j+2] = -v;
todo = true;
}
}
}
// step 2: mark all three-algined candy to negative with **left and right** directions
for (int j = 0; j < n; ++j) {
for (int i = 0; i < m-2; ++i) {
int v = abs(board[i][j]);
if (v != 0 && v == abs(board[i+1][j]) && v == abs(board[i+2][j])) {
board[i][j] = -v;
board[i+1][j] = -v;
board[i+2][j] = -v;
todo = true;
}
}
}
// step 3: gravity part
if (todo) {
for (int j = 0; j < n; ++j) {
int row = m-1; // pointing at bottom
for (int i = m-1; i >= 0; --i) { // shift down
if (board[i][j] > 0)
board[row--][j] = board[i][j];
}
while (row >= 0) // fill the original candy loc to 0
board[row--][j] = 0;
}
return candyCrush(board);
}
return board;
}
};