0987. Vertical Order Traversal of a Binary Tree¶
Given a binary tree, return the vertical order traversal of its nodes values.
For each node at position (X, Y), its left and right children respectively will be at positions (X-1, Y-1) and (X+1, Y-1).
Running a vertical line from X = -infinity to X = +infinity, whenever the vertical line touches some nodes, we report the values of the nodes in order from top to bottom (decreasing Y coordinates).
If two nodes have the same position, then the value of the node that is reported first is the value that is smaller.
Return an list of non-empty reports in order of X coordinate. Every report will have a list of values of nodes.
Example 1:
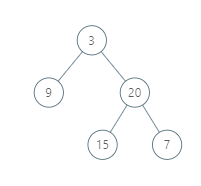
Input: [3,9,20,null,null,15,7]
Output: [[9],[3,15],[20],[7]]
Explanation:
Without loss of generality, we can assume the root node is at position (0, 0):
Then, the node with value 9 occurs at position (-1, -1);
The nodes with values 3 and 15 occur at positions (0, 0) and (0, -2);
The node with value 20 occurs at position (1, -1);
The node with value 7 occurs at position (2, -2).
Example 2:
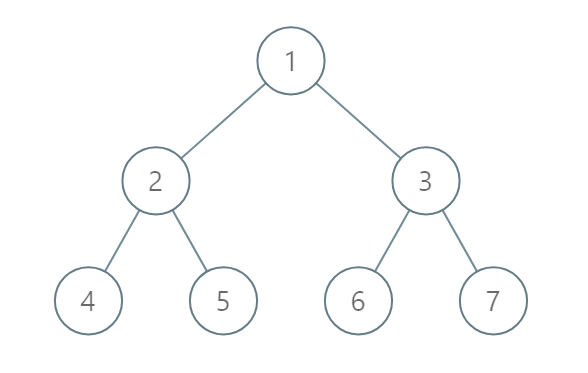
Input: [1,2,3,4,5,6,7]
Output: [[4],[2],[1,5,6],[3],[7]]
Explanation:
The node with value 5 and the node with value 6 have the same position according to the given scheme.
However, in the report "[1,5,6]", the node value of 5 comes first since 5 is smaller than 6.
Note:
- The tree will have between 1 and
1000nodes. - Each node's value will be between
0and1000.
Analysis¶
To obtain the vertical order, we first need to understand how to "order" all the nodes in each vertical level. If we mark the root node as level 0, then for all the nodes on the left will be: -1, -2, -3 … -n. Vice versa, for all the nodes on the rght will be 1, 2, 3 … n. Depending on the position of the nodes, we can categorize all the nodes base on the level.
However, there is one thing to be consider: if two nodes are on the same vertical and horizontal level (see last test case), we have to sort the nodes base on their value. This is a special case we need to consider, and thus besides the vertical order, we also need to record the horizontal order. To do so, we need a sorted map which looks like:
{vertical level, {horizonal level, sorted value}}
Which yield: map<int, map<int, set<int>> (here we assume all the nodes have different values, if there could have same values, then we can use multiset).
- Time: $ O(n)$ since need to traverse all the nodes
- Space: O(n) since need to store all the nodes
Code¶
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> verticalTraversal(TreeNode* root) {
map<int, map<int, set<int>>> nodes;
queue<tuple<TreeNode*, int, int>> todo;
todo.push({root, 0, 0});
while (!todo.empty()) {
auto [node, x, y] = todo.front();
todo.pop();
nodes[x][y].insert(node -> val);
if (node -> left) {
todo.push({node -> left, x - 1, y + 1});
}
if (node -> right) {
todo.push({node -> right, x + 1, y + 1});
}
}
vector<vector<int>> ans;
for (auto p : nodes) {
vector<int> col;
for (auto q : p.second) {
col.insert(col.end(), q.second.begin(), q.second.end());
}
ans.push_back(col);
}
return ans;
}
};