0994. Rotting Oranges

You are given an m x n grid where each cell can have one of three values:

• 0 representing an empty cell,
• 1 representing a fresh orange, or
• 2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

Example 1:

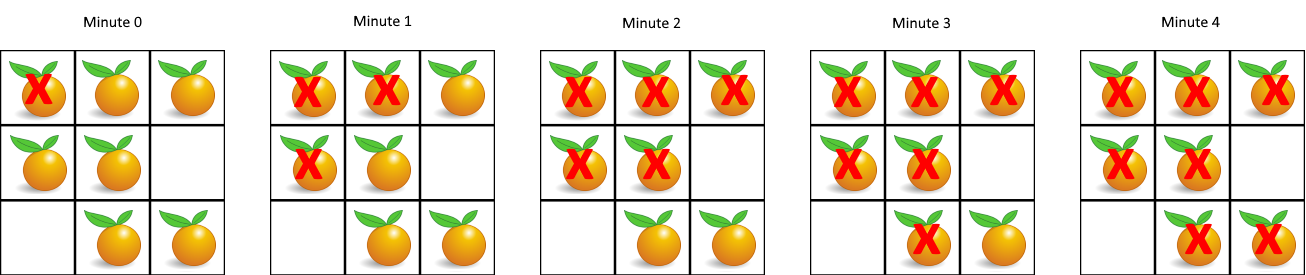
Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Example 2:

Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 3:

Input: grid = [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10
• grid[i][j] is 0, 1, or 2.

Analysis

Using bfs to expand level by level, using a counter to keep track of how many levels are there, which is the anser of our problem.

• Time Complexity: $O(N)$ since you need to iterate through all the cells.
• Space Complexity: $O(N)$ since the worst case is when you put all the 1s into the queue.

Code

class Solution {
public:
    int orangesRotting(vector<vector<int>>& g) {
        // step 1: check if possible
        int m = g.size(), n = g[0].size();
        queue<pair<int, int>> q;
        vector<pair<int, int>> ones;
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j) {
                if (g[i][j] == 2)
                    q.push({i,j});
                else if (g[i][j] == 1) 
                    ones.push_back({i,j});
            }
        // step 2: iterate all the neigbours who are currently 1
        int dir[4][2] = {{0,1},{0,-1},{1,0},{-1,0}};
        int minutes = 0;
        while (!q.empty()) {
            minutes ++;
            int sz = q.size();
            for (int i = 0; i < sz; ++i) {
                int x, y;
                tie(x, y) = q.front();
                q.pop();
                for (auto d : dir) {
                    int dx = x + d[0], dy = y + d[1];
                    // error check and then set to 2 and put it to queue
                    if (dx < 0 || dx >= m || dy < 0 || dy >= n || 
                        g[dx][dy] != 1) continue;
                    g[dx][dy] = 2;
                    q.push({dx,dy});
                }
            }
        }
        // step 3: error checking
        for (auto coord : ones)
            if (g[coord.first][coord.second] == 1) return -1;
        // if answer is 0, then return 0
        return max(0, minutes - 1);
    }
};

---

Last update: April 1, 2022